Meta Pseudo Label: ImageNet Top1 Accuracy 90% 達成!
前言
2021 年 1 月 Google Brain 的 Principal Scientist — Quoc Le 在個人 Twitter 帳號上宣佈首次在 ImageNet Benchmark 上達到了 Top 1 Accuracy 90% 的成績,也讓 Meta Pseudo Label 這篇命運多舛的 Paper 搖身一變成為 State-of-the-Art 的作品。

Meta Pseudo Label (簡稱 MPL) 這篇 Paper 於一年前 2020/3 第一次出現在 ArXiv 。雖然身為 Semi-Supervised Learning 主題的文章 (SSL 當時正熱門呢),MPL 一開始並沒有受到太多關注,尚有一些理論與實務上瑕疵的地方。例如直接利用 Validation Loss 來訓練模型,或是硬是用了 Meta Learning 框架來解釋 Gradient 的走向 (但筆者認為 MPL 的核心精神更加貼近 Reinforcement Learning 中的 Actor-Critic) 。
隨著 Paper 的不斷改寫,在最新的 v4 (arXiv:2003.10580v4) 中,Paper 作者已有詳細推導 Student (Actor) 與 Teacher (Critic) Model 是如何交互作用,以嚴謹的數學說明 MPL 是如何拿下 ImageNet SOTA 的成績,而非以往認知 Semi-Supervised Learning 靠著龐大的資料與混合的 Regularization 取勝。
本篇文章會仔細介紹 MPL 的數學推導,說明 Teacher-Student 之間是如何相輔相成,希望能讓大家都欣賞到 MPL 精妙的設計。
Semi-Supervised Learning (SSL) 成為主流
攤開近年 ImageNet Benchmark,可以明顯看到 SSL 屠榜的趨勢。

在 2018 年之前,主要的進步來自於架構的改善; 在 EfficientNet 被發明 (或者說發現) 後架構就沒有大幅進步了,研究則轉向由 Data-Driven,也就是 SSL 演算法的改進。

究竟 SSL 的表現有多強呢?
讓我們觀察 Second-tier 的榜單 (84%~85%) 。這個區間多為 Network Architecture 的改善 (藍色標記),但很明顯的,改架構的效益極為有限 (<1%); 但伴隨的 Model Size (#params) 與 FLOPS 影響很巨大。相較之下,利用 Noisy-Student SSL 演算法與大量 Unlabeled Data 訓練的 EfficientNet-B3 (橘色標記) ,能以輕量的架構達到相同水準。例如與 ResNet-RS-350 相差近兩個數量級,相當不講武德。


另外 SSL 也我們看到 Neural Network 的 Capcaity 其實相當高,就像經典的 ResNet-50 到現在還沒被資料 “塞滿”,依舊能不斷進步。
Self-Training Framework
首先,我們比較 Noisy-Student 與 MPL 的架構。
Noisy-Student 演算法:
- 在 Labeled Data 上訓練 Teacher Model
- 由 Teacher 在 Unlabeled Data 上標記出 Pseudo Label 作為 Student 的訓練資料
- 因為 Pseudo Label 很髒 ,Student 訓練時需要加上各種 Regularization 方法避免 Confirmation Bias
- Student Model 作為下一個 Iteration 的 Teacher Model
以上演算法構成了一個 Open Loop 的 Self-Training 框架,Teacher 並不知道 Student 的學習狀況,Student 也僅是靠著 RandAug, Stochastic Depth 種種高強度的 Regularization 避免學壞。
MPL 的目標是解決 Teacher-Student 缺乏互動的問題

MPL 演算法構建了一個 Closed Loop (或稱 Feedback Loop) 訓練框架,也就是說,Teacher Model 會根據 Student 的學習狀況做調整。
- 由 Teacher 在 Unlabeled Data 上標記出 Pseudo Label 作為 Student 的訓練資料
- Teacher 根據 Student 的學習狀況來更新自己,讓下一個 Iteration 能標記出更適合 Student 學習的 Pseudo Label
以上就是 MPL 演算法的概念,也就是 Update Teacher 時同時考慮 Student。接下來我們將逐步構建出他的 Training Algorithm。
延伸思考
- MPL 可以類比 Reinforcement Learning 中 Agent 與 Environment 的關係,action 與 reward 類比為 pseudo label 與 student signal
- 在 Noisy-Student 中 Teacher 與 Student Model 的地位其實是等價的,因為一個 Iteration 後會發生取代; 在 MPL 中 Teacher 與 Student Model 其實不等價,Teacher 只作為 Data 的容器 (data distribution) ,因此在 Paper 附錄中衍伸出 Economical version of MPL — 用一個 multi-layer perceptron 透過學習 Identity map 來充當 Teacher Model 。此部分本文不展開討論,留給讀者思考玩味。
MPL 演算法推導 — Part I
由於 MPL 是數學上嚴謹的演算法,這意味著枯燥與乏味 (笑),我們分為 3 個部分,從不同面向切入,讓讀者能循序漸進的了解 MPL。
Cross Entropy Loss
畢竟 MPL 還是 Image Classification 問題,使用的 Loss 是經典的 Cross Entropy Loss 。本文要特別強調的是 Target Distribution ,在不同的 Training Scheme 會選用不同的表示,例如 One-Hot 用於 Supervised Learning; Soft-Label 常用於 SSL 等等。Target Distribution 的選擇對 MPL 帶來深遠的影響。

另外,讀者可以留意本文中 Cross Entropy 用了兩種表示 L(theta) 與 CE(target, predict),前者強調 Model 後者強調 Prediction。另外下標 l 表示 對 labeled data 計算 loss; 下標 u 代表 unlabeled data 。
Pseudo Label as Bi-Level Optimization Problem
要建構演算法,就要定義 Teacher 與 Student 是如何溝通的。我們將之前的概念轉換為以下兩條 Update Rules
Rule 1 — Student Update Rule: 用 Teacher 給出 Pseudo Label 來訓練 Student

Rule 2 — Teacher-Student Update Rule: 用 Student 在 Labeled Data 上的表現作為回饋,來修正 Teacher 的教導能力

把兩條式子放在一起,就是我們 MPL Training Problem

但這個 Training Problem 實務上很困難的,有兩個地方需要簡化。
簡化一:在 Student 的 Update Rule 中,Teacher 以 Soft-Label 的形式直接出現在 Loss Function ,意味著整個 Teacher Model 會出現在 Back-propagation Graph 中,會造成訓練非常緩慢 (想像一下 Teacher 也是 EfficientNet-L2) 。
解決的方法是將 Soft-Label 轉為 Hard-Label ,由於 ArgMax Operator 不可微分,能直接 Break End-to-end Path。
簡化二:在 Teacher-Student Update Rule 中,Teacher 直接與 Student Model 耦合在一起,成為很複雜的 Optimization Problem,實務上需要把耦合去除。
因此 Paper 中利用了簡化的技巧 (可以說 One-Step Update 或者 First-order Taylor Expansion) ,將原本 Student 受 Teacher 影響而耦合的式子展開,成為簡單的 Gradient Update Rule ,並且可以利用前一步 Student Update Rule 的結果來替換。

經過實務上的簡化,我們能得到較詳細的關係圖如下:

Teacher 靠著 Pseudo Label 把資訊傳給 Student,同時做 Harden Pseudo Label 降低運算量;透過 Reused Student’s Update,更新 Teacher 使他更能因材施教。

以上就是 MPL 的演算法,Paper 的正文也是描述到這邊。基本上交代了一個自洽也合理的流程,讓大家都明白訓練目標與做法。但同時也留下一些困惑與實務上的含糊,而本文的目的就是說明這些細節。
問題
- 簡化二 宣稱 Decouple 了原本的 Teacher-Student Update,說好的師生互動是怎麼樣實踐的?
- Reuse Student’s Update 是什麼意思?是直接用 Student’s Weights 取代 Teacher’s Weights 嗎?
- 把 Soft Pseudo Label 轉成 Hard Pseudo Label 造成什麼影響?
- Teacher 負責標記 Unlabeled Data,但 Teacher 有從中獲得資訊來修正自己嗎? 還是全靠 Labeled Data?
- Student 出現在 Rule 1 與 2 ,到底 Student Inference 幾次 Update 幾次?
現在,讓我們進入 Part II 來看看 MPL 真實的面貌。
MPL 演算法推導 — Part II
MPL 最困難的在於如何 Rule2 — Update Teacher-Student (當一個顧慮到學生的老師真難),本節直接推導 Update Teacher-Student 的 Gradient 並將在 Part III 以演算法的形式再次說明。
推導過程
為了維持閱讀愉快,推導完整過程位於本文末,更詳細過程也可以參考原始 Paper 附錄。
推導結果
我們直接上結果。以數學表達相當漂亮,Teacher-Student Update Rule 如下:

我們逐項來說明:
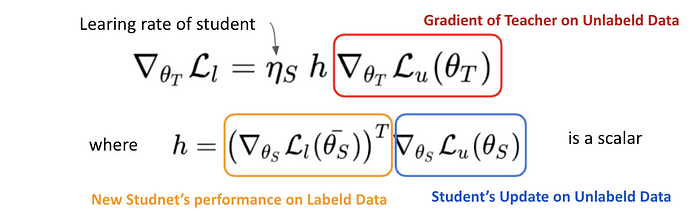
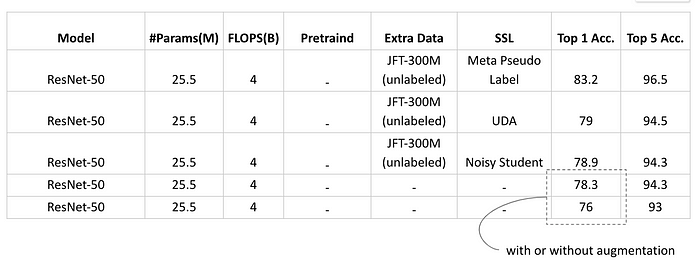
- 左式是 Gradient of Teacher-Student Update on Labeled Data,意義為根據 Student 在 Labeled Data 上面的表現,修正 Teacher 的教育方式
- Gradient of Teacher-Student Update 其實與 Gradient of Teacher (on Unlabeled Data) 向量平行:意味著 Teacher 本身能不能在 Unlabeled Data 上標出好的結果直接影響 Teacher-Student 的關係 (Teacher 多會教,直接影響師生的關係)
- Teacher-Student Gradient 跟 Student Learning Rate 成正比
- Teacher-Student Gradient 與一個常量 h 成正比 — 這個常量 (scalar) 就是 Student Model 是否有進步的指標 (Student Feedback Signal)
- h (Student Feedback Signal) 為兩個 Gradient 內積:分別是原本 Student 在 Unlabeled Data 上的表現與 Update 過後的 Student 在 Labeled Data 讓的表現內積
MPL 演算法推導 — Part III
最後,脫離複雜的數學公式,我們從直觀的演算法與流程圖再次理解 MPL 。
演算法
從 Part II 詳細地推導 (於文末) ,我們列出各項 Gradient 的來源,並且逐步在演算法實作中取得他們。(為了方便,我們用顏色區分需計算的每項,一直到文末顏色都保持一致的)

首先,我們寫下演算法的 Pseudo Code 如下:

接著,我們用圖示來說明以上演算法動態時發生什麼事情。
Gradient Flow
規則:虛線為 Forward; 實線為 Backprop 取得 Gradient; 若有相同顏色線條形成 Loop 代表 Model 被 Update。
Step 1:Teacher Model Inference Unlabeled Data,產生一組 Pseudo Label,並且轉成 Hard-Label 。

Step 2: Student Model Forward & Backward on Unlabeled Data,並且 Update 。也就是 Rule1 — Student Update。

Step 3:Student Inference Labeled Data 計算 並且 Backward 取得 Gradient ,注意這裡沒有形成 Loop 因此 Student Model 並不會因為這次 Backprop 而更新。此外 Reuse Student’s Update 算出 Student Feedback Signal h 。

Step 4 -1:Teacher Model 再次 Inference Unlabeled Data 並且計算 Gradient。注意,這裡容易會產生盲點,因為 Unlabeled Data 是 Teacher 自己標記出來的,為什麼能算出 Non-Zero Loss 並且 Backprop 呢?原因正是因為 Step 1 已經將 Pseudo Label 轉為 Hard-Label,計算 Cross Entropy 時還是能算出結果。算出紅色 Gradient 後與 h 相乘。

Step 4–2:Teacher Model Inference Labeled Data 並 Backward 計算 Gradient。

Step 4–3 :最後把 Teacher Model 的 Loop Close 起來,一次 Update Teacher Model。完成一個 MPL Step 。

延伸討論
回答先前的問題
- 師生互動體現在微分後的 Jacobian Matrix,最後化成藍色與紅色的 Gradient
- Reuse Student’s Update 指的就是藍色 Gradient 後來計算 h 可以重複使用
- Teacher 會從中自己標出的 Hard Label 與 Soft Label 間產生 Loss 而且合併 Student Feedback 來 Update
- Student 其實 Inference 了兩次,但第二次只取 Gradient 並不會 Update Model (有趣的是 Student 並不直接透過 Labeled Data Training)
- 如果使用 Soft Pseudo Label,基本上就完全不適用這裡推導的所有公式,而整個問題應該可以 End-to-end Training
那,為什麼非得做 Hard Pseudo Label 呢?用 Soft Pseudo Label 會有問題嗎?
除了免除 End-to-end 很龐大以外,筆者認為當計算 CE(q, p) Prediction 與 Target 皆為 Soft-Label 時,Cross Entropy 並沒有辦法真正拉近兩個 Distribution 的距離,因為 Divergence 公式表明 KL = CE(q, p) - H(q),如果單純用 CE 可能無法防止 Teacher Model 產生 High Entropy 模稜兩可的 Pseudo Label; 相較之下,Hard-Label 則強迫 Teacher 做出明確的決定。
結論
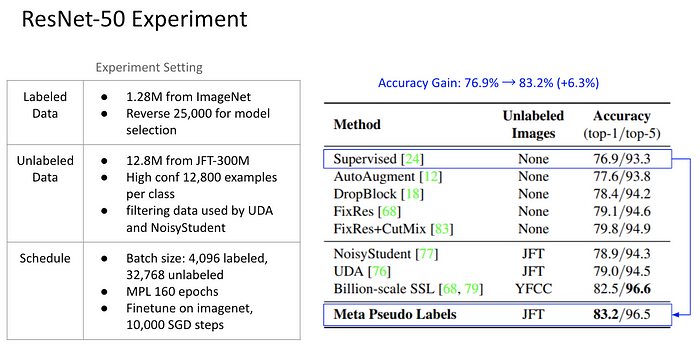
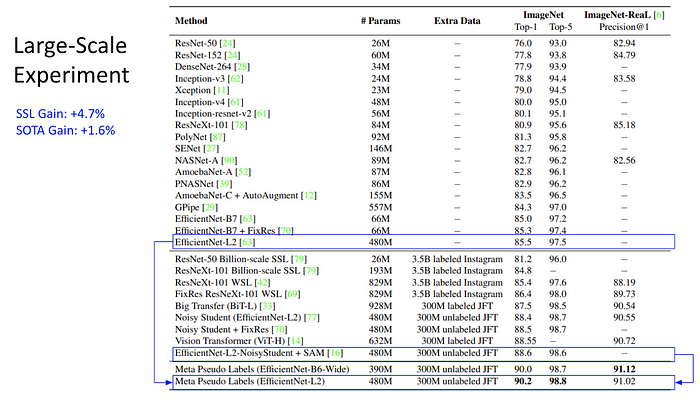
以上,就是 MPL 的詳細運作過程。從實驗中我們可以看到他的效果非常顯著; 此外,在數學推導上本篇也是有相當嚴謹,並提出合理的訓練框架,可以說 SOTA 的結果是靠著演算法的進步所拿下的。
附錄
資料: Labeled Data 與 Unlabeled Data
在本文與實驗中提到的 Labeled Data 均為 ImageNet; Unlabeled Data 為 JFT-300M。讀者可以注意數量級即可,Unlabeled Data 圖片數量為 Labeled Data 的 100 倍 (JFT 300M 中取 130M 來用),約有 20% 是帶有 noise 的。

Teacher-Student Update Rule 推導過程
首先,是一個數學上的建模。引入一個 Estimator 作為 Updated Student 的數學模型 (因為 Student Update 以後變成什麼樣子,並不能完全知道,所以我們用他的平均行為來描述)。接著就是暴力微分:

根據 Chain Rule 與變數變換,我們能得到一個 Jacobian Matrix ,它也就是最重要的一項 (藍色框框),描述了 Student Model 如何因為 Teacher Model 而改變。

接這是一些變數的合併與整理,讓我們比較好看。
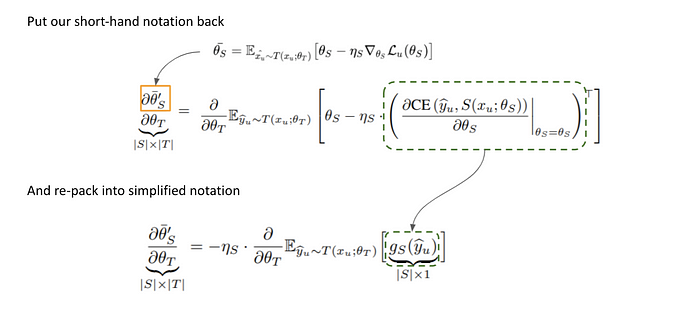
整理過後,一個對 Estimator 中 Distribution 微分的形式出現了,而他與 Reinforcement Learning 中常用到的 Policy Gradient 如出一轍。因此我們可以用這個公式替換,最後整理出 Cross Entropy 的形式。

由於我們 Harden Pseudo Label — Break End-to-End Path,當要微分時跟 RL 中要對 Expected Reward 計算 Policy Gradient 是一樣的道理。

最後我們把得到的各項放在一起,可以求得最後的 Teacher-Student Gradient。
References
- Self-training with Noisy Student improves ImageNet classification, https://arxiv.org/abs/1911.04252
- Meta Pseudo Labels, https://arxiv.org/abs/2003.10580
- MPL Source Code: https://github.com/google-research/google-research/tree/master/meta_pseudo_labels
- 筆者報告的投影片:https://docs.google.com/presentation/d/19Oii6bs2UKg8rsgfG4mY42BHT3x3T8KQzbWjpqoGCnc/edit#slide=id.p